or any consecutive p numbers.

This system is called a complete system of numbers incomparable in modulus p or a complete system of modulo deductions p. Obviously, all sorts of p consecutive numbers form such a system.

All numbers belonging to the same class have many common properties, therefore, in relation to the modulus, they can be considered as one number. Each number included in a comparison as a summand or a factor can be replaced, without violating the comparison, by a number comparable to it, i.e. with a number belonging to the same class.

Another element that is common to all numbers of a given class is the greatest common divisor of each element of that class and module p.

Let a And b comparable in modulus p, Then

Theorem 1. If in ax+b instead of x let's substitute everything sequentially p members of the complete number system

Therefore all numbers ax+b, Where x=1,2,...p-1 are not comparable in modulus p(V otherwise, numbers 1,2,... p-1 would be comparable in modulus p.

Notes

1) In this article, the word number will be understood as an integer.

Literature

• 1. K. Ireland, M. Rosen. A classic introduction to modern number theory. − M: Mir, 1987.
• 2. G. Davenport. Higher arithmetic. − M: Nauka, 1965.
• 3. P.G. Lejeune Dirichlet. Lectures on number theory. − Moscow, 1936.

Clause 17. Complete and reduced systems of deductions.

In the previous paragraph it was noted that the relationship є m comparability modulo arbitrary m is an equivalence relation on the set of integers. This equivalence relation induces a partition of the set of integers into classes of elements equivalent to each other, i.e. numbers that when divided by m identical balances. Number of equivalence classes є m(experts will say - "equivalence index є m") is exactly equal m .

Definition. Any number from the equivalence class є m we will call it modulo residue m. A set of deductions taken one from each equivalence class є m, is called a complete system of modulo residues m(in the full system of deductions, therefore, only m pieces of numbers). The remainders themselves when divided by m are called the smallest non-negative residues and, of course, form a complete system of modulo residues m. A residue r is called absolutely the smallest if it is the smallest among the modules of residues of a given class.

Example: Let m= 5 . Then:

0, 1, 2, 3, 4 - the smallest non-negative residues;

2, -1, 0, 1, 2 are the absolute smallest deductions.

Both given sets of numbers form complete systems of modulo residues 5 .

Lemma 1. 1) Any m pieces that are not comparable in modulus m numbers form a complete system of modulo residues m .

2) If A And m are relatively simple, and x m, then the values ​​of the linear form ax+b, Where b- any integer, also run through the complete system of modulo residues m .

Proof. Statement 1) is obvious. Let us prove statement 2). Numbers ax+b smooth m things. Let us show that they are not comparable in modulus m. Well let it be for some different x 1 And x 2 from the complete system of deductions it turned out that ax 1 +b є ax 2 +b(mod m). Then, according to the properties of comparisons from the previous paragraph, we get:

ax 1 є ax 2 (mod m)

x 1 є x 2 (mod m)

- a contradiction with the fact that x 1 And x 2 are different and taken from the complete system of deductions.

Since all numbers from a given equivalence class є are obtained from one number of a given class by adding a number that is a multiple m, then all numbers from this class have modulus m the same greatest common divisor. For some reasons, of increased interest are those deductions that have with the module m greatest common divisor equal to one, i.e. residues that are coprime to the modulus.

Definition. The reduced system of modulo deductions m is the set of all residues from the complete system that are coprime to the modulus m .

The reduced system is usually chosen from the smallest non-negative residues. It is clear that the given system of modulo residues m contains j( m) pieces of deductions, where j ( m) – Euler function – the number of numbers less than m and coprime with m. If by this point you have already forgotten the Euler function, look at paragraph 14 and make sure that something was said about it there.

Example. Let m= 42. Then the given system of residues is:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Lemma 2. 1) Any j ( m) numbers that are pairwise incomparable in modulus m and coprime with the modulus, form a reduced system of modulo residues m .

2) If (a,m) = 1 And x runs through the reduced system of modulo residues m, That ax also runs through the reduced system of modulo residues m .

Proof. Statement 1) is obvious. Let us prove statement 2). Numbers ax are pairwise incomparable (this is proven in the same way as in Lemma 1 of this paragraph), there are exactly j of them ( m) things. It is also clear that all of them are relatively prime to the modulus, because (a,m)=1, (x,m)=1 Yu (ax.m)=1. So the numbers ax form a reduced system of residues.

These are the definitions and basic properties of the complete and reduced systems of residues, however, in the stock of mathematical knowledge there is also a whole series very interesting and useful facts regarding deduction systems. If you keep silent about them at this point, then this, I’m afraid, will be a direct violation of the Law Russian Federation about Information, malicious concealment of which is, according to this law, an administrative and even criminal offense. In addition, without familiarity with further important properties of deduction systems, paragraph 17 will turn out to be very scanty. Let's continue.

Lemma 3. Let m 1, m 2, ..., m k– are pairwise relatively prime and m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k, Where

1) If x 1 , x 2 , ..., x k run through complete systems of residues modulo m 1, m 2, ..., m k accordingly, then the values ​​of the linear form M 1 x 1 +M 2 x 2 + ...+M k x k run through the complete system of modulo deductions m=m 1 m 2 ...m k .

2) If x 1 , x 2 , ..., x k run through the reduced residue systems modulo m 1, m 2, ..., m k accordingly, then the values ​​of the linear form M 1 x 1 +M 2 x 2 + ...+M k x k run through the reduced system of modulo residues m=m 1 m 2 ...m k .

Proof.

1) Shape M 1 x 1 +M 2 x 2 + ...+M k x k obviously accepts m 1 m 2 ...m k =m values. Let us show that these values ​​are pairwise incomparable. Well let it be

M 1 x 1 +M 2 x 2 + ...+M k x k є M 1 x 1 С +M 2 x 2 С + ...+M k x k С (mod m)

All sorts of things M j, different from M s, multiple m s. Removing terms on the left and right in the last comparison that are multiples m s, we get:

M s x s є M s x s С (mod m s) У x s є x s С (mod m s)

- a contradiction with the fact that xs runs through the complete system of modulo residues m s .

2). Form M 1 x 1 +M 2 x 2 + ...+M k x k obviously takes j ( m 1) j ( m 2) Ch ... Ch j ( m k) = j ( m 1 m 2 H ... H m k)= j ( m) (Euler's function is multiplicative!) of different values, which modulo each other m=m 1 m 2 ...m k pairwise incomparable. The latter is easily proven by reasoning similar to the reasoning carried out in the proof of statement 1) of this lemma. Because ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s ,m s)=1 for everyone 1 Ј s Ј k, That ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=1, hence the set of values ​​of the form M 1 x 1 +M 2 x 2 + ...+M k x k forms a reduced system of modulo residues m .

Lemma 4. Let x 1 , x 2 , ..., x k ,x run full, and x 1 , x 2 ,..., x k , x– run through the given systems of residues modulo m 1, m 2, ..., m k And m=m 1 m 2 ...m k respectively, where (m i m j)=1 at i No. j. Then fractions (x 1 /m 1 +x 2 /m 2 +...+x k /m k) coincide with fractions (x/m), and fractions ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k ) coincide with fractions (x/m) .

Proof. The proof of both statements of Lemma 4 is easily obtained by applying the previous Lemma 3 after you have given each sum (x 1 /m 1 +x 2 /m 2 +...+x k /m k) And ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k ) to a common denominator:

(x 1 /m 1 +x 2 /m 2 +...+x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ;

( x 1 /m 1 + x 2 /m 2 +...+ x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ,

Where M j =m 1 ...m j-1 m j+1 ...m k .

If we now take into account that the fractional parts of the numbers obtained when divided by the modulus m any two numbers comparable in modulus m, are the same (they are equal r/m, Where r is the smallest non-negative residue from a given class), then the statements of this lemma become obvious.

In the rest of this section, the most interesting thing will happen - we will sum the complex roots m-th power of unity, and we will discover amazing connections between sums of roots, systems of residues and the already familiar multiplicative Möbius function m ( m) .

Let us denote by e k k th root m- oh power of unity:

We remember these forms of writing complex numbers well from our first year. Here k=0,1,...,m-1– runs through the complete system of modulo deductions m .

Let me remind you that the amount e 0 + e 1 +...+ e m-1 all roots m the th power of one is equal to zero for any m. Indeed, let e 0 + e 1 +...+ e m-1 =a. Let's multiply this sum by a non-zero number e 1. Such multiplication geometrically in the complex plane means rotating the correct m-a triangle with roots at its vertices e 0 , e 1 ,..., e m-1, to a non-zero angle 2p/m. It is clear that in this case the root e 0 will go to the root e 1, root e 1 will go to the root e 2, etc., and the root e m-1 will go to the root e 0, i.e. sum e 0 + e 1 +...+ e m-1 will not change. We have e 1 a=a, where a=0 .

Theorem 1. Let m>0- integer, a O Z , x runs through the complete system of modulo residues m. Then if A multiple m, That

otherwise, if A not a multiple m ,

.

Proof. At A multiple m we have: a=md And

At A not divisible by m, divide the numerator and denominator of the fraction a/m on d– greatest common divisor A And m, we get an irreducible fraction a 1 /m 1. Then, by Lemma 1, a 1 x will run through the complete system of modulo deductions m. We have:

because the sum of all roots of the degree m 1 from one is equal to zero.

Let me remind you that the root e k m the th power of unity is called antiderivative if its index k coprime with m. In this case, as was proven in the first year, successive degrees e k 1 , e k 2 ,..., e k m-1 root e k form the entire set of roots m-th power of one or, in other words, e k is the generating element of the cyclic group of all roots m-th power of unity.

Obviously, the number of different primitive roots m the th power of unity is equal to j ( m), where j is the Euler function, since the indices of the antiderivative roots form a reduced system of modulo residues m .

Theorem 2. Let m>0– an integer, x runs through the modulo reduced system of residues m. Then (sum of antiderivative roots of degree m):

where m ( m) – Möbius function.

Proof. Let m=p 1 a 1 p 2 a 2 ...p k a k– canonical expansion of a number m ; m 1 =p 1 a 1 , m 2 =p 2 a 2 , m 3 =p 3 a 3; x i runs through the reduced system of modulo residues m i. We have:

At a s =1 it turns out that only the root e 0 =1 is not antiderivative, therefore the sum of all antiderivative roots is the sum of all roots minus one:

therefore, if m free from squares (i.e. not divisible by r 2, at r >1), That

If any indicator a s greater than one (i.e. m divided by r 2, at r>1), then the sum of all antiderivative roots of the degree m s is the sum of all roots of the degree m s minus the sum of all non-prime roots, i.e. all roots of some degree less m s. Exactly if m s =p s m s *, That:

Now, dear readers, when I have presented for your consideration quite a significant amount of information about the complete and given systems of deductions, no one can accuse me of maliciously violating the Law of the Russian Federation on Information by concealing it, so I finish this paragraph with satisfaction.

Problems

1 . Write down on a piece of paper all the smallest non-negative residues and all the absolutely smallest residues a) modulo 6, b) modulo 8. Just below write down the given systems of deductions for these modules. Draw the sixth and eighth roots of unity separately on the complex plane, circle the primitive roots in both drawings and find their sum in each case. 2 . Let e– primitive root of the degree 2n from one. Find the amount: 1+ e + e 2 +...+ e n-1 . 3 . Find the sum of all primitive roots: a) 15th; b) 24th; c) the 30th power of one. 4 . Find the sum of all possible products of primitive roots n-th power from one, taken in twos. 5 . Find the amount k-x powers of all roots n-th power of unity. 6 . Let m>1 , (a, m)=1 , b– integer, X runs through the complete, and x – reduced system of modulo residues m. Prove that: A) b) 7 . Prove that: , Where r runs through all prime factors of a number A .

Clause 17. Complete and reduced systems of deductions.

In the previous paragraph it was noted that the relationship є m comparability modulo arbitrary m is an equivalence relation on the set of integers. This equivalence relation induces a partition of the set of integers into classes of elements equivalent to each other, i.e. numbers that when divided by m identical balances. Number of equivalence classes є m(experts will say - "equivalence index є m") is exactly equal m .

Definition. Any number from the equivalence class є m we will call it modulo residue m. A set of deductions taken one from each equivalence class є m, is called a complete system of modulo residues m(in the full system of deductions, therefore, only m pieces of numbers). The remainders themselves when divided by m are called the smallest non-negative residues and, of course, form a complete system of modulo residues m. A residue r is called absolutely the smallest if it is the smallest among the modules of residues of a given class.

Example: Let m= 5 . Then:

0, 1, 2, 3, 4 - the smallest non-negative residues;

2, -1, 0, 1, 2 are the absolute smallest deductions.

Both given sets of numbers form complete systems of modulo residues 5 .

Lemma 1. 1) Any m pieces that are not comparable in modulus m numbers form a complete system of modulo residues m .

2) If A And m are relatively simple, and xm, then the values ​​of the linear form ax+b, Where b- any integer, also run through the full system of modulo residues m .

Proof. Statement 1) is obvious. Let us prove statement 2). Numbers ax+b smooth m things. Let us show that they are not comparable in modulus m. Well let it be for some different x 1 And x 2 from the complete system of deductions it turned out that ax 1 +b є ax 2 +b(mod m). Then, according to the properties of comparisons from the previous paragraph, we get:

ax 1 є ax 2 (mod m)

x 1 є x 2 (mod m)

- a contradiction with the fact that x 1 And x 2 are different and taken from the complete system of deductions.

Since all numbers from a given equivalence class є are obtained from one number of a given class by adding a number that is a multiple m, then all numbers from this class have modulus m the same greatest common divisor. For some reasons, of increased interest are those deductions that have with the module m greatest common divisor equal to one, i.e. residues that are coprime to the modulus.

Definition. The reduced system of modulo deductions m is the set of all residues from the complete system that are coprime to the modulus m .

The reduced system is usually chosen from the smallest non-negative residues. It is clear that the given system of modulo residues m contains j( m) pieces of deductions, where j ( m) – Euler function – the number of numbers less than m and coprime with m. If by this point you have already forgotten the Euler function, look at paragraph 14 and make sure that something was said about it there.

Example. Let m= 42. Then the given system of residues is:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Lemma 2. 1) Any j ( m) numbers that are pairwise incomparable in modulus m and coprime with the modulus, form a reduced system of modulo residues m .

2) If (a,m) = 1 And x runs through the reduced system of modulo residues m, That ax also runs through the reduced system of modulo residues m .

Proof. Statement 1) is obvious. Let us prove statement 2). Numbers ax are pairwise incomparable (this is proven in the same way as in Lemma 1 of this paragraph), there are exactly j of them ( m) things. It is also clear that all of them are relatively prime to the modulus, because (a,m)=1, (x,m)=1 Yu (ax.m)=1. So the numbers ax form a reduced system of residues.

These are the definitions and basic properties of the complete and reduced systems of residues, however, in the baggage of mathematical knowledge there is a number of very interesting and useful facts concerning systems of residues. If you keep silent about them in this paragraph, then this, I’m afraid, will be a direct violation of the Law of the Russian Federation on Information, malicious concealment of which is, according to this law, an administrative and even criminal offense. In addition, without familiarity with further important properties of deduction systems, paragraph 17 will turn out to be very scanty. Let's continue.

Lemma 3. Let m 1, m 2, ..., m k– are pairwise relatively prime and m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k, Where

1) If x 1 , x 2 , ..., x k run through complete systems of residues modulo m 1, m 2, ..., m k run through the complete system of modulo deductions m=m 1 m 2 ...m k .

2) If x 1 , x 2 , ..., x k run through the reduced systems of residues modulo m 1, m 2, ..., m k accordingly, then the values ​​of the linear form run through the reduced system of modulo residues m=m 1 m 2 ...m k .

Proof.

1) Shape M 1 x 1 +M 2 x 2 + ...+M k x k obviously accepts m 1 m 2 ...m k =m values. Let us show that these values ​​are pairwise incomparable. Well let it be

M 1 x 1 +M 2 x 2 + ...+M k x k є M 1 x 1 С +M 2 x 2 С + ...+M k x k С (mod m)

All sorts of things M j, different from M s, multiple m s. Removing terms on the left and right in the last comparison that are multiples m s, we get:

M s x s є M s x s С (mod m s) У x s є x s С (mod m s)

- a contradiction with the fact that xs runs through the complete system of modulo residues m s .

2). Form M 1 x 1 +M 2 x 2 + ...+M k x k obviously takes j ( m 1) j ( m 2) Ch ... Ch j ( m k) = j ( m 1 m 2 H ... H m k)= j ( m) (Euler's function is multiplicative!) of different values, which modulo each other m=m 1 m 2 ...m k pairwise incomparable. The latter is easily proven by reasoning similar to the reasoning carried out in the proof of statement 1) of this lemma. Because ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s ,m s)=1 for everyone 1 Ј s Ј k, That ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=1, hence the set of values ​​of the form M 1 x 1 +M 2 x 2 + ...+M k x k forms a reduced system of modulo residues m .

Lemma 4. Let x 1 , x 2 , ..., x k ,x run full, and x 1 , x 2 ,..., x k , x– run through the given systems of residues modulo m 1, m 2, ..., m k And m=m 1 m 2 ...m k respectively, where (m i m j)=1 at i No. j. Then fractions coincide with fractions (x/m), and fractions coincide with fractions (x/m) .

Proof. The proof of both statements of Lemma 4 is easily obtained by applying the previous Lemma 3 after you have given each sum (x 1 /m 1 +x 2 /m 2 +...+x k /m k) And ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k ) to a common denominator:

(x 1 /m 1 +x 2 /m 2 +...+x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ;

( x 1 /m 1 + x 2 /m 2 +...+ x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ,

Where M j =m 1 ...m j-1 m j+1 ...m k .

If we now take into account that the fractional parts of the numbers resulting from division by the modulus m any two numbers comparable in modulus m, are the same (they are equal r/m, Where r is the smallest non-negative residue from a given class), then the statements of this lemma become obvious.

In the rest of this section, the most interesting thing will happen - we will sum the complex roots m-th power of unity, and we will discover amazing connections between sums of roots, systems of residues and the already familiar multiplicative Möbius function m ( m) .

Let us denote by e k k th root m- oh power of unity:

We remember these forms of writing complex numbers well from our first year. Here k=0,1,...,m-1– runs through the complete system of modulo deductions m .

Let me remind you that the amount e 0 + e 1 +...+ e m-1 all roots m the th power of one is equal to zero for any m. Indeed, let e 0 + e 1 +...+ e m-1 =a. Let's multiply this sum by a non-zero number e 1. Such multiplication geometrically in the complex plane means rotating the correct m-a triangle with roots at its vertices e 0 , e 1 ,..., e m-1, to a non-zero angle 2p/m. It is clear that in this case the root e 0 will go to the root e 1, root e 1 will go to the root e 2, etc., and the root e m-1 will go to the root e 0, i.e. sum e 0 + e 1 +...+ e m-1 will not change. We have e 1 a=a, where a=0 .

Theorem 1. Let m>0- integer, a O Z , x runs through the complete system of modulo residues m. Then if A multiple m, That

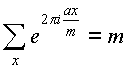
otherwise, if A not a multiple m ,

.

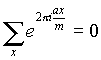Proof. At A multiple m we have: a=md And

At A not divisible by m, divide the numerator and denominator of the fraction a/m on d– greatest common divisor A And m, we get an irreducible fraction a 1 /m 1. Then, by Lemma 1, a 1 x will run through the complete system of modulo deductions m. We have:

because the sum of all roots of the degree m 1 from one is equal to zero.

Let me remind you that the root e k m the th power of unity is called antiderivative if its index k coprime with m. In this case, as was proven in the first year, successive degrees e k 1 , e k 2 ,..., e k m-1 root e k form the entire set of roots m-th power of one or, in other words, e k is the generating element of the cyclic group of all roots m-th power of unity.

Obviously, the number of different primitive roots m the th power of unity is equal to j ( m), where j is the Euler function, since the indices of the antiderivative roots form a reduced system of modulo residues m .

Theorem 2. Let m>0– an integer, x runs through the modulo reduced system of residues m. Then (sum of antiderivative roots of degree m):

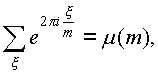
where m ( m) – Möbius function.

Proof. Let m=p 1 a 1 p 2 a 2 ...p k a k– canonical expansion of a number m ; m 1 =p 1 a 1 , m 2 =p 2 a 2 , m 3 =p 3 a 3; x i runs through the reduced system of modulo residues m i. We have:

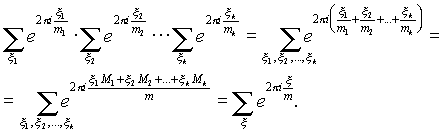
At a s =1 it turns out that only the root e 0 =1 is not antiderivative, therefore the sum of all antiderivative roots is the sum of all roots minus one:

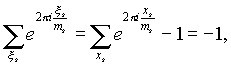
therefore, if m free from squares (i.e. not divisible by r 2, at r >1), That

If any indicator a s greater than one (i.e. m divided by r 2, at r>1), then the sum of all antiderivative roots of the degree m s is the sum of all roots of the degree m s minus the sum of all non-prime roots, i.e. all roots of some degree less m s. Exactly if m s =p s m s *, That:

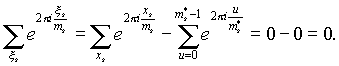
Now, dear readers, when I have presented for your consideration quite a significant amount of information about the complete and given systems of deductions, no one can accuse me of maliciously violating the Law of the Russian Federation on Information by concealing it, so I finish this paragraph with satisfaction.

Problems

1 . Write down on a piece of paper all the smallest non-negative residues and all the absolutely smallest residues a) modulo 6, b) modulo 8. Just below write down the given systems of deductions for these modules. Draw the sixth and eighth roots of unity separately on the complex plane, circle the primitive roots in both drawings and find their sum in each case. 2 . Let e– primitive root of the degree 2n from one. Find the amount: 1+ e + e 2 +...+ e n-1 . 3 . Find the sum of all primitive roots: a) 15th; b) 24th; c) the 30th power of one. 4 . Find the sum of all possible products of primitive roots n-th power from one, taken in twos. 5 . Find the amount k-x powers of all roots n-th power of unity. 6 . Let m>1 , (a, m)=1 , b– integer, X runs through the complete, and x – reduced system of modulo residues m. Prove that: A) b) 7 . Prove that: , Where r runs through all prime factors of a number A .

A set of numbers comparable to a modulo m called class of numbers modulo m(or equivalence class). All numbers of one class have the form mt+ r at fixed r.

For a given m, r can take values ​​from 0 to m-1, i.e. everything exists m classes of numbers modulo m, and any integer will fall into one of the modulo classes m. Thus,

Z= m m … [m-1]m, Where [ r]m={x Z: x≡r(mod m)}

Any number of class [ r]m called minus modulo m in relation to all numbers of the same class. Number equal to remainder r, called smallest non-negative deduction.

The deduction that is smallest in absolute value is called absolutely the smallest deduction.

Example

Let's take the module m=5. And let a=8. Let's divide a on m with remainder:

Remainder r=3. This means 8 5, and the smallest non-negative residue of the number 8 modulo 5 is 3.

The absolute smallest deduction can be found by calculating r-m=3-5=-2, and comparing the absolute values ​​|-2| and |3|. |-2|<|3|, значит -2 – абсолютно наименьший вычет числа 8 по модулю 5.

Taking one deduction from each class, we get full system of deductions modulo m. If all these numbers are the smallest non-negative modulo residues m, then such a system of deductions is called complete system of least non-negative residues, and is denoted by Z m.

{0; 1;…; m-1) = Z m– a complete system of least non-negative residues.

(– ;…; 0;…; ) (if m–odd number) ;

( - ,…,-1, 0, 1,…, ) or (- ,…, -1, 0, 1,…, ) (if m even number) is a complete system of absolutely least residues.

Example

If m=11, then the complete system of least non-negative residues is (0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10), and the complete system of absolutely least residues is (–5; –4; –3 ; –2; 0; 2;

Statement 1

Any m numbers that are pairwise incomparable in modulus m, form a complete system of residues for this module.

Proof:

Indeed, due to incomparability, these numbers belong to different classes, and since their m pieces, then each existing class contains exactly one number.

Statement 2

If ( a, m) = 1, and x runs through the complete system of modulo residues m, That ax+b, Where b– any number from Z also runs through the complete system of modulo residues m.

Proof:

Numbers ax+b it will be smooth m things. It remains to prove that any 2 numbers ax 1 +b And ax 2 +b incomparable in modulus m, If x 1 x 2 (mod m)

Proof by contradiction. Let's assume that ax 1 +b≡ ax 2 +b(mod m) due to the 4th holy of comparisons, ax 1 ≡ ax 2 (mod m) due to the nature of comparisons No. 9 and the fact that ( a, m) = 1, we have x 1 ≡ x 2 (mod m). We got a contradiction with the fact that x 1 x 2 (mod m). Therefore, the assumption is false, which means the opposite is true. That is ax 1 +b And ax 2 +b incomparable in modulus m, If x 1 x 2 (mod m), which was what needed to be proven.

As shown in §5, the relation of comparability modulo m has the properties of reflexivity, symmetry and transitivity; therefore it is an equivalence relation. Take an arbitrary integer a. Let us denote by o the set of numbers comparable to a modulo m: Let. Let it be now. And so on. The process will continue until the constructed sets cover the entire set of integers. In this case, a partition of the set Z into sets a arises. b, c,..which are called residue classes modulo m; each number included in any of the classes is called a residue of this class. The number of residue classes modulo m is equal to m. Indeed, the remainder of dividing an integer by m takes one of the values ​​m - 2 or m - 1 and therefore each of the numbers falls into one of the classes 01, the number of which is equal to m. Taking one number from of each class of residues we obtain a system of representatives of the classes of residues, or a complete system of residues modulo m. Systems of residues Example 1. Various complete systems of residues modulo 7: Lemma 3. Numbers xm form a complete system of residues modulo m if and only if they are pairwise incomparable modulo m. The necessity is obvious. Let's prove the sufficiency. If two numbers are not comparable modulo then they fall into different residue classes. Since there are m classes of residues in total and the numbers under consideration are mn, they constitute a complete system of residues. Lemma 4. Let xm be a complete system of residues modulo m, an integer a coprime with m, b an arbitrary integer. Then the numbers axi + 6, ax2 + b, ..axm -f b also form a complete system of residues. According to Lemma 3, it is enough to verify that Suppose (to lead to a contradiction) h OG general definition the relationship and its properties will be discussed below - in Chapter LXVIII; Note that number theory is the source of many important examples for general algebra. Partitioning a set is representing it as a union of pairwise disjoint subsets. Then a(xi-xj) \my and, since (o, m) = 1, we have (Xi-Xj) m, which contradicts Lemma 3. Lemma 5. Let x = a(modm). Then (Systems of residues m Indeed, let r be the remainder of the division of o by m. Then, by Lemma 2 But since x = a(mod m), when divided by m, "elo g" there has a remainder r, and, therefore, (i,t) = (r,t), from which the required follows. So, numbers from the same class of residues modulo m have the same greatest common divisor with m. Therefore, the following definition becomes correct. Residue modulo m is called reduced if it is coprime with m. The set of reduced residues from different classes of residues is called a reduced system of residues. Example 2. For m = 7, a reduced system of residues can look like this: Systems of residues The Euler function (p(t)) is the number of natural numbers, not. exceeding m and mutually simple with m. For example, . It is easy to see that if p is a prime number, Obviously, the reduced system of residues modulo m contains numbers. Lemma 6. Let a be a relatively simple reduced system of residues modulo m. Then the numbers ax. \, ax k also form a reduced system of residues modulo m. 4 Since the numbers o and X( are coprime to m, their product ax* also has the same property. By Lemma 4, the numbers ax\,ax2,... belong to different classes of residues, and, therefore, by virtue of the previous one, they form a reduced system of residues.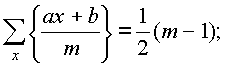
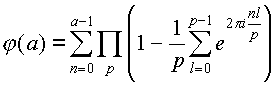